Zad. 1. Wewnątrz trójkąta równoramiennego (gdzie |AC|=|BC|) obrano punkt K taki, że |∡KAB|=|∡KBC|. Wiedząc, że |∡AKM|=28° (gdzie M jest środkiem boku AB), znajdź miarę kąta CKB.
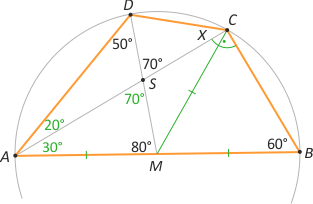
Zad. 2. W czworokącie ABCD przekątna AC przecina odcinek DM (gdzie M jest środkiem boku AB) w punkcie S. Wiedząc, że |∡ADM|=50°, |∡DSC|=70°, |∡AMD|=80° oraz |∡ABC=60°|, znajdź miarę kąta ACD.
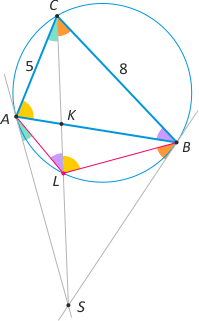
Zad. 3. W okrąg wpisano trójkąt ABC. Styczne do okręgu w punktach A i B przecinają się w punkcie S. Prosta CS przecina bok AB w punkcie K. Wiedząc, że |BC|=8 i |AC|=5, oblicz |AK|:|KB|.
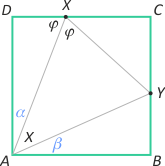
Zad. 4. (wolna amerykanka) Dany jest kwadrat i dwa dowolne punkty X i Y leżące odpowiednio na bokach CD i BC. Wiedząc, że AX jest dwusieczną kąta DXY, znajdź miarę kąta XAY.
W tym miesiącu za zadania 1-3 punkty otrzymali:
- 30 - Iwona Gruszecka (nauczycielka w CLV LO Warszawa), Mikołaj Popek (student UAM) i Tadeusz Porzucek (emerytowany nauczyciel z Gostynia;
- 20 - Elżbieta Grzechnik (emerytowana nauczycielka z Radomia), Szymon Kaźmierowski (nauczyciel z Elbląga), Marzena Wąsiewicz (nauczycielka z Kajetan), Janusz Wieczorek (emerytowany nauczyciel z Sandomierza).
Za zadanie 4 po 10 pkt. otrzymali: Iwona Gruszecka, Szymon Kaźmierowski, Zygmunt Krawczyk (emerytowany nauczyciel ze Szprotawy), Szymon Meyer (analityk danych z Dziewkowic), Mikołaj Popek, Tadeusz Porzucek, Marzena Wąsiewicz i Janusz Wieczorek.
Gratulujemy!
Zad. 1. Zbudujmy na boku BC trójkąt CBN przystający do trójkąta AKB. Mamy |AC|=|BC|,
|CK|=|CN| oraz |AK|=|BN|. Trójkąt CKN jest równoramienny i podobny do trójkąta ABC, bo mają ten sam kąt przy wierzchołku C. Zatem |∡CKN| = α +β. Przedłużmy środkową KM do punktu L takiego, że |ML|=|KM|. Otrzymujemy równoległobok ALBK, w którym |∡KLB|=28°. Zauważmy, że trójkąty LBK i KBN są przystające (na mocy cechy bkb). Stąd |∡KNB|=28°. Ostatecznie |∡CKB| = α+β+180°–(28°+α+β) = 152°.
Zad. 2. Łatwo zauważyć, że trójkąt ABC jest prostokątny, a środkowa CM ma długość taką, jak odcinki AM i MB. Ponadto trójkąt AMD jest równoramienny, przy czym |AM|=|MD|. Oznacza to, że punkty A, B, C i D leżą na jednym okręgu o środku M, a stąd kąt wpisany ACD ma miarę 40°.
Zad. 3. Łatwo zauważyć pary kątów o równych miarach (żółte i fioletowe - kąty wpisane w okrąg oparte na tych samych łukach oraz zielone i pomarańczowe - kąty wpisane i dopisane oparte na tych samych łukach). Mamy zatem cztery pary trójkątów podobnych: (1) SAL i SAC, (2) SBL i SBC, (3) AKL i KBC oraz (4) AKC i KLB. Z tych podobieństw wynikają proporcje:
(1) |AL|:|LS| = |AC|:|AS| i (2) |BL|:|LS| = |BC|:|BS|. Dzieląc je stronami i uwzględniając, że
|AS|=|BS|, otrzymujemy (*) |AL|:|BL| = |AC|:|BC|. Z kolejnych podobieństw mamy proporcje: (3) |AK|:|CK| = |AL|:|BC| oraz (4) |KB|:|KC| = |BL|:|AC|. Dzieląc je stronami i stosując (*), otrzymujemy |AK|:|KB| = (|AC|:|BC|)2 = 25/64.
Zad. 4. Zauważmy, że |AX| = a/cosα i |AY| = a/cosβ. Dalej mamy φ = 90°–α i |∡XAY| = 90°–(α+β), a stąd |∡AYX| = 2α+β. Stosując twierdzenie sinusów w trójkącie AYX, otrzymujemy
|AX|:sin(2α+β) = |AY|:sin(90°–α), a po podstawieniu za AX i AY równość przyjmuje postać a:sin(2α+β)cosα = a:cosα·cosβ. Stąd otrzymujemy sin(2α+β) = cosβ = sin(90°–β). Ostatecznie 2α+β = 90°–β, czyli α+β = 45°, zatem szukany kąt X ma miarę 45°.
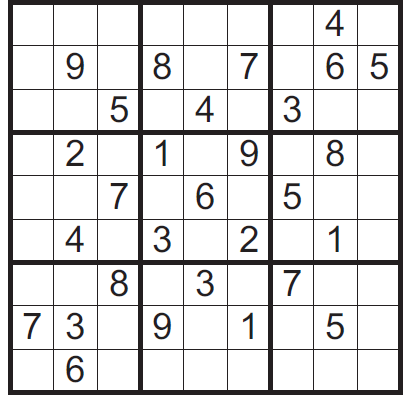
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
